Notched Boxplots

3-groups Comparison Example
3-groups Simulation
Many Groups Simulation

Aim: demonstrate advantages and disadvantages of notched bloxplots
boxplot help page: “if notch is TRUE, a notch is drawn in each side of the boxes. If the notches of two plots do not overlap this is ‘strong evidence’ that the two medians differ (Chambers et al, 1983, p. 62)”
“The notches (if requested) extend to +/-1.58 IQR/sqrt(n). This seems to be based on the same calculations as the formula with 1.57 in Chambers et al (1983, p. 62), given in McGill et al (1978, p. 16). They are based on asymptotic normality of the median and roughly equal sample sizes for the two medians being compared, and are said to be rather insensitive to the underlying distributions of the samples. The idea appears to be to give roughly a 95% confidence interval for the difference in two medians.”

3-groups Comparison Example

3 variables (x,y,z)
normal distribution
different means and same standard deviation
investigate effect of n

library(gridBase)
library(gridExtra)
library(grid)

layout(matrix(c(1,1,2,3,3,4,5,5,6), nrow = 3, ncol = 3, byrow = F))


ns <- c(10,40,90)

for(i in seq_along(ns)){
    
    n <- ns[i]
    
    set.seed(123)
    
    x <- rnorm(n, 0)
    y <- rnorm(n, 0.55)
    z <- rnorm(n, -0.25)
    
    dat <- data.frame(outcome = c(x,y,z),
                      group = rep(c("X","Y","Z"), each = n))
    
    
    boxplot(outcome ~ group, data = dat, 
            notch = TRUE, ylim = c(-1,1),
            main = paste("n =", n))
    
    rect(xleft = 0, ybottom = median(x)-IQR(x, type = 2)*1.58/sqrt(n), 
         xright = 4, ytop =   median(x)+IQR(x, type = 2)*1.58/sqrt(n), 
         border = NA, col = "#00000033")
    
    rect(xleft = 0, ybottom = median(y)-IQR(y, type = 2)*1.58/sqrt(n), 
         xright = 4, ytop =   median(y)+IQR(y, type = 2)*1.58/sqrt(n), 
         border = NA, col = "#00000033")
    
    
    rect(xleft = 0, ybottom = median(z)-IQR(z, type = 2)*1.58/sqrt(n), 
         xright = 4, ytop =   median(z)+IQR(z, type = 2)*1.58/sqrt(n), 
         border = NA, col = "#00000033")
    
    # fit anova
    fit <- aov(outcome ~ group, data = dat)
    
    # perform Tukey test
    tukey_results <- TukeyHSD(fit, ordered = TRUE)$group
    
    # formatting
    tukey_results[,1:3] <- round(tukey_results[,1:3], 2)
    tukey_results[,4] <- format(tukey_results[,4], digits = 2, scientific = T)
        
    # tricks to plot table
    frame()
    vps <- baseViewports()
    pushViewport(vps$inner, vps$figure, vps$plot)
    grob <-  tableGrob(tukey_results, theme=ttheme_default(base_size = 10))  
    grid.draw(grob)
    popViewport(3)
}

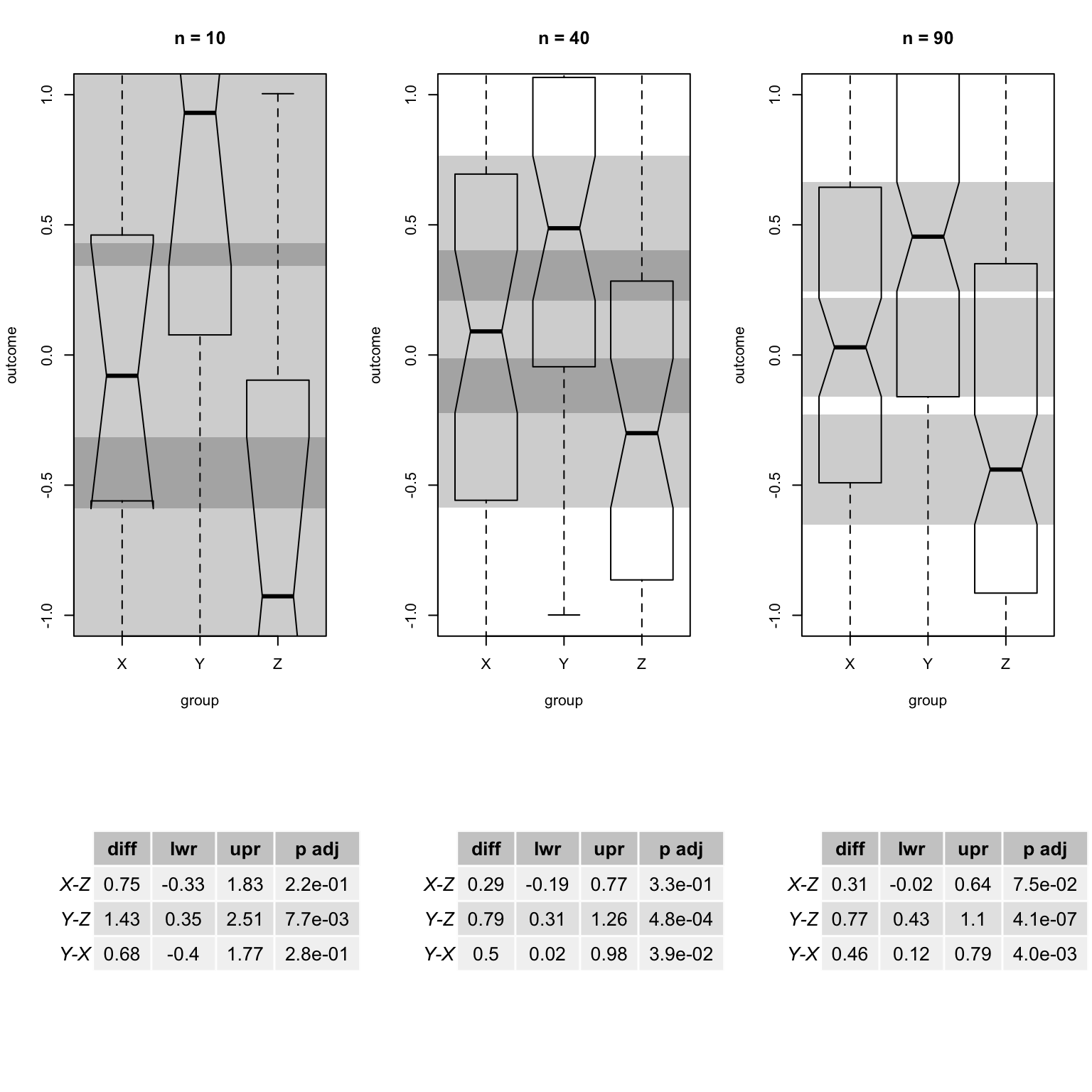
as expected notch intervals decrease with increased n
n = 10, X-Y and X-Z notches overlap and only Y-Z is significant (notches do not overlap)
n = 40, X-Y and X-Z notches overlap and Y-Z as well as X-Y is significant
n = 90, none of the notches overlap but X-Z is not significant
notch overlap is not always consistent with Tukey test

3-groups Simulation

3 groups, show only X-Y comparison

n = 40

n_overlap1 <- replicate(1000, expr = {
    
    x <- rnorm(n, 0)
    y <- rnorm(n, 0.55)
    # no need for z (notches are constructed independently)
    
    x_upr <- median(x)+IQR(x, type = 2)*1.58/sqrt(n)
    x_lwr <- median(x)-IQR(x, type = 2)*1.58/sqrt(n)
    y_upr <- median(y)+IQR(y, type = 2)*1.58/sqrt(n)
    y_lwr <- median(y)-IQR(y, type = 2)*1.58/sqrt(n)
    
    !(x_lwr > y_upr | x_upr < y_lwr)
    
})


n_overlap2 <- replicate(1000, expr = {
    
    x <- rnorm(n, 0)
    y <- rnorm(n, 0.55)
    z <- rnorm(n, -0.25)
    
    dat <- data.frame(outcome = c(x,y,z),
                      group = rep(c("X","Y","Z"), each = n))
    
    fit <- aov(outcome ~ group, data = dat)
    tukey_results <- TukeyHSD(fit, ordered = FALSE)$group
    
    tukey_results["Y-X",2] < 0  & tukey_results["Y-X",3] > 0
})


mean(n_overlap1); mean(n_overlap2)

## [1] 0.66

## [1] 0.468

it is more frequent that the notch intervals overlap than the Tukey intervals overlap 0
in such setup we would find more often significant results using Tukey test

Many Groups Simulation

few additional Zs

n = 40

n_overlap1 <- replicate(1000, expr = {
    
    x <- rnorm(n, 0)
    y <- rnorm(n, 0.55)
    # no need for z (notches are constructed independently)
    
    x_upr <- median(x)+IQR(x, type = 2)*1.58/sqrt(n)
    x_lwr <- median(x)-IQR(x, type = 2)*1.58/sqrt(n)
    y_upr <- median(y)+IQR(y, type = 2)*1.58/sqrt(n)
    y_lwr <- median(y)-IQR(y, type = 2)*1.58/sqrt(n)
    
    !(x_lwr > y_upr | x_upr < y_lwr)
})



n_overlap2 <- replicate(1000, expr = {
    
    x <- rnorm(n, 0)
    y <- rnorm(n, 0.55)
    z1 <- rnorm(n, -0.25)
    # add manually some Zs
    z2 <- rnorm(n, -0.25)
    z3 <- rnorm(n, -0.25)
    z4 <- rnorm(n, -0.25)
    z5 <- rnorm(n, -0.25)
    z6 <- rnorm(n, -0.25)
    z7 <- rnorm(n, -0.25)
    z8 <- rnorm(n, -0.25)
    
    dat <- data.frame(outcome = c(x,y,z1,z2,z3,z4,z5,z6,z7,z8),
                      group = rep(c("X","Y","Z1","Z2","Z3","Z4","Z5","Z6","Z7","Z8"), each = n))
    
    fit <- aov(outcome ~ group, data = dat)
    tukey_results <- TukeyHSD(fit, ordered = FALSE)$group
    
    tukey_results["Y-X",2] < 0  & tukey_results["Y-X",3] > 0
})


mean(n_overlap1); mean(n_overlap2)

## [1] 0.661

## [1] 0.751

constructing the notch intervals does not take into account the number of groups/comparisons
by adding more groups Tukey intervals more frequently include 0 (not significant)

Conclusions:

notch intervals are conservative when having a few groups only
they are not corrected for multiple tests, so with many groups it becomes anti-conservative
due this behavior notched boxplot can only be used as a quick exploratory tool